이번 포스팅에서는 저번 포스팅에 이어 무선 절편과 무선 기울기를 추가하는 것이 어떤 의미를 가지는지 다룬다.
저번 포스팅부터 보면 조금 더 도움이 될 것 같다!
2023.03.27 - [통계 공부/Linear Mixed Effects Model] - Brauer & Curtin(2018) 논문: 무선 절편과 무선 기울기
Brauer & Curtin(2018) 논문: 무선 절편과 무선 기울기
이번 포스팅에서는 무선 절편과 무선 기울기의 개념을 예를 통해 간단히만 다룰 것이다. 저번 포스팅에서 데이터가 비독립적일 때 에러 항이 여러 성분으로 나뉘게 된다고 적었다. 그러면서 어
psstat.tistory.com
비독립적 데이터에서 무선 절편과 무선 기울기가 무선 효과라고 불린다고 했다.
그 이유는 전집들 중에서 무선적으로 나타나는 효과이기 때문인데,
이는 고정 효과(β0와 β1)의 계수가 무선 변인의 서로 다른 수준에서 달라질 수 있음을 말한다.
예를 들어, 명망의 절편과 독립변인의 효과가 A참가자와 B참가자에게서 달라질 수 있다는 것이다.
●무선 절편의 추가

식으로 살펴보자.
식 (1)은 절편은 절편끼리, Χ항은 Χ항끼리 정리한 식이다.
이 중 β0는 전체 평균 선호도(grand mean)를, u0j는 β0에 비교하여 달라지는 참가자의 평균 선호도를 나타낸다.
참고로 i는 아이템을, j는 참가자를 나타낸다.
무슨 말인지 좀 더 자세히 살펴보자.

위의 그림에서 빨간색 선은 높은 명망 조건, 파란색 선은 낮은 명망 조건에 대한 종속반응이라 가정하자
(실제로는 다른 논문에서 가져온 그림이다).
세모는 높은 명망 조건에 대한, 동그라미는 낮은 명망 조건에 대한 각 참가자의 실제 데이터를 나타낸다.
현재는 아무런 무선 효과가 반영되지 않은 그림인데 u0j를 추가하면 어떤 일이 벌어질까?
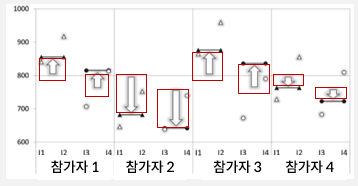
기존 모형에 무선 절편을 추가하면 조건 간 차이는 그대론데
각 참가자 별로 자신의 평균 선호도만큼만 전반적인 반응이 이동하게 된다.
위의 그림을 보면 한 참가자 내에서는 화살표가 움직이는 크기가 똑같은데
각 참가자 별로는 움직이는 화살표의 크기가 다른 것을 확인할 수 있다.
이는 각 참가자의 평균 선호도만큼만 화살표가 움직였기 때문이다.
이렇게 무선 절편을 모형에 추가하여 생기는 장점은 오차가 감소하여 β1의 민감도가 증가한다는 것이다.
●무선 기울기의 추가

이제 독립변인(예에서는 명망)의 효과에 관한 Xij를 살펴보자.
이 항도 절편처럼 두 개로 구성되어 있다.
하나는 독립변인에 대한 고정효과(즉, β1)이고,
나머지 하나(u1j)는 참가자들마다 이 고정효과가 달라짐을 명시하는 항이다.

앞서 모형에 무선 절편을 추가했기 때문에 각 참가자들마다 평균적인 반응이 달라지는 것이 고려되었다.
하지만 세모 막대와 동그라미 막대의 차이(간격)는 모든 참가자에게서 똑같은 것을 확인할 수 있다.
즉, 독립변인인 명망의 효과가 모든 참가자에게서 똑같이 고정되어있는 것이다.
여기에서 참가자에 대한 무선 기울기를 추가하면 아래와 같이 그림이 바뀐다.

이제 각 참가자마다 세모 막대와 동그라미 막대의 차이가 달라진 것을 알 수 있다.
여기서 우리는 무선 기울기를 투입하는 것이 독립변인의 효과가 참가자마다 다름을 모형에 명시하는 것임을 알 수 있다.
<잡담>
무선 절편과 무선 기울기를 투입하는 것이 어떤 의미를 갖는지 시각적으로 잘 보여주는 예시가 있어서 가져와봤는데
이해하는데 도움이 되었길 바란다.
혹시 본문에 틀린 내용이 있거나 잘 이해가 안 가는 부분이 있다면 댓글 달아주시길 바란다.
'통계 공부 > Linear Mixed Effects Model' 카테고리의 다른 글
| Brauer & Curtin(2018) 논문: 둘 이상의 독립변인 (0) | 2023.03.30 |
|---|---|
| Brauer & Curtin(2018) 논문: 무선변인과 무선효과의 구분 (0) | 2023.03.29 |
| Brauer & Curtin(2018) 논문: 무선 절편과 무선 기울기 (0) | 2023.03.27 |
| Brauer & Curtin(2018) 논문: 에러 항 구조 비교 (0) | 2023.03.25 |
| Brauer & Curtin(2018) 논문: 용어 정리 (0) | 2023.03.24 |